In 1687, Isaac Newton (1642-1727) produced his famous and important work 'Principia', based on the experiments and analysis of Galileo Galilei (1564-1642). In this work he proposed three main laws. The first was the law of inertia. He used the term inertia for the property of matter that causes it to resist a change in its state of motion. Inertia of an object must be overcome to set it in motion. The measure of an objects' inertia is its mass. The law of inertia states: "If the net force on an object is zero (i.e. if the vector sum of all forces acting on the object is zero), then the acceleration of the object is zero and the object moves with constant velocity."
Fnet = 0
Newton's second law states: "The accelerated motion of a body can only be produced by the application of a force to that body. The direction of the acceleration is the same as the direction of the force and the magnitude of the acceleration is proportional to the magnitude of the force."
F = ma
Commonly, the F is referred to as weight, w. The acceleration, a, is referred to as g or gravity, on Earth 9.81 m/s2.
Newton's third law tells that single forces cannot occur. Forces always act in pairs. It states: "If object 1 exerts a force on object 2, then object 2 exerts an equal force, oppositely directed, on object 1."
F12 = -F21
All forces have a direction and a magnitude, force is a vector quantity. The SI unit of force (F) is the Newton. One Newton (N) is the unit mass (kg) times the unit acceleration (m/s2). Obviously these three laws also apply to microgravity, or better, acceleration research.
Gravity is, besides the weak nuclear force, the strong nuclear force and the electrostatic force, one of the four basic forces described in nature today. Among these forces, gravity is by far the weakest. Compared to an unit gravity or hypergravity environment, various physical phenomena behave differently in the, theoretical, state of zero acceleration, also known as weightlessness. In our universe there is only a theoretical zero gravity since there is mass in outer space, hence, gravity fields, as is shown by Newton's 'universal law of gravitation'.
FG = G (mM/r2)
Where:
FG = the gravitational force
G = the gravitational constant (=6.67x10-11 Nm2/kg2)
m = mass of object
M = mass of the Earth
r = distance between the center of the two masses m and M.
In theory there is, in our Universe, no such thing as zero gravity. Since there are masses present everywhere there is gravity. In an orbiting spacecraft such as the Space Shuttle or Mir these is also a small gravity residuum due to various reasons. A typical spacecraft would experience atmospheric drag (6-30·10-7g, at 250 km), solar radiation pressure (±5·10-9g), gravity gradient of extended bodies not located in the center of mass (±5·10-9g) and finally self gravitation due to its own mass (±10-9g).(Minster 1993, Otto)
Principle of Equivalence
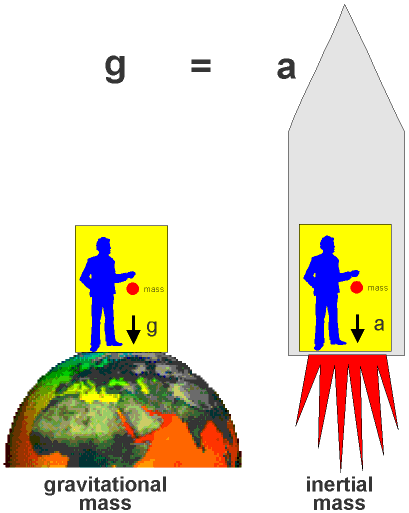
An important aspect of Einstein's' general relativity has to do with the equivalence of gravitational fields and accelerated motion. If we are in a laboratory on Earth, a mass that is released will fall, or accelerate, downward due to the gravitational attraction of the Earth. Now, let us move this laboratory into space, away from the gravitational influence of a planet. We now take the same object and release it within an accelerating rocket. The level of acceleration of the rocket, a, is the same as the Earth gravity, g. In such a situation the rocket will 'push' onto the laboratory floor and move this floor towards the 'falling' mass. As far as the observations of the two motions of the mass relative to the floor are concerned, the accelerated motion in the two cases will be exactly the same. If the laboratory would have no windows, the observer could not distinguish between an acceleration due to gravity (e.g. on Earth) and an acceleration due to a 'push' of e.g. a rocket in space. Or as Einstein described it some 70 years ago in his 'principle of equivalence':
"In a closed laboratory, no experiment can be performed that will distinguish between the effects of a gravitational field and the effects due to an acceleration with respect to some inertial reference frame."
(To learn more about the Equivalence Principle you may visit the ESA STEP (Satellite Test of the Equivalence Principle) mission page.)

Figure: Difference between 'gravitational mass'(mG) and 'inertial mass' (mI). The observer would see no difference between the two accelerations, hence mG = mI.
It was only at the onset of space
exploration and the possibility to perform experiments in free falling capsules
that we can perform so called 'microgravity' or better 'microweight' experiments.
The possibility to compensate the on Earth ever present gravitational force
provides us very useful tool and an unique experiment environment to study possible
effects of gravity on living systems, humans, animals, plants, cells or even
smaller structures.
Before the time we could actually perform spaceflight experiments there were
some reports that stated that, on a cellular level, gravity, either micro or
hypo-gravity or hypergravity, would have no effect on these systems. One of
the first papers on the physical background of microgravity studies on a cellular
level was written by Pollard nearly thirty years ago. In this very illustrative
work he evaluates phenomena like temperature, Brownian movement, convection,
hydrostatic forces, and stresses experienced by a cell membrane. He concluded
that cells with a diameter of 10 µm and up would experience gravity. This
effect would be due do the redistribution of nucleoli or mitochondria. Although
comparing various forces and energies present within living cells may be very
illustrative, their magnitude is not necessarily related to their impact. The
extent of various cellular physicochemical phenomena has been described in a
very illustrative assay by Albrecht-Buehler. (Albrecht-Buehler 1991) In this
paper the author relates the micro-environment of cells with the macro-environment
where we, as human beings, relate to. It is calculated that the force of gravity
is 400,000 times smaller then the force of surface tension, and the force for
moving only one single electron in a typical electrical field of a nerve cell
membrane is comparable to the weight of an entire cell. Water appears to be
very viscous on a cellular level, while the impact energy, by Brownian movement,
of only three water molecules is comparable to the weight of an entire cell.
The gravitational potential energy of a cell due to gravity is about 21 kJ/mole,
while the chemical energy of only one hydrogen bound is 17 kJ/mole. Finally
the contractile force of a single sarcomere is comparable to the weight of 60
cells. Also the force of polymerization is far more powerful than the weight
of a single cell, while the force needed to add only one sub-unit of for example
microfilaments, is about ten times larger than the weight of a cell.
All these theoretical studies indicate that, on a (sub-) cellular level gravity
would have no impact whatsoever. However, there have been numerous studies,
both on orbiting spacecraft and in ground based facilities, that indicate that
gravity does have an effect on small systems. (See for review Moore & Cogoli,
1996). What the mechanism of this phenomenon is, is still a matter of debate.
Only future experiments on board Shuttle, ISS as well as in ground based facilities
might reveal some of the mechanisms involved.
Artificial gravity
Since gravity, or acceleration, is a vectorial entity, we can produce 'artificial gravity' to change direction of the vector. This can be done in a centrifuge. In a constantly rotating centrifuge the object moves with a constant velocity. However, since the orientation is also constantly changed the object is accelerated.
ac = w2r
Where:
ac = centripetal acceleration (m/s2)
w = angular velocity (rad/s)
r = radius (m)
The force on this object would be a centripetal force:
Fc = mac = mw2r
One of the often made mistakes about microgravity and space flight is to presume that the presence of microgravity in orbiting spacecraft, such as the Shuttle or the future International Space Station, is due to the fast that 'they are in space' or 'outside the Earth's atmosphere. Although it might seem that these spacecraft are 'far' away for human perspective they are actually quite close by to Earth, only 300-500 km from the Earth's surface. So if it is not the fact of being up there, what is it ?
. . . . . . . . It is . . . . . . FREE FALL . . . . . . . .
These spaceships or satellites actually fall around the Earth. In fact, if the Earth's surface would be as smooth as a snooker ball it would be possible to provide microgravity in a capsule that circulates the Earth's surface at a distance of just one millimeter. For a typical Shuttle mission at an altitude of e.g. 350 km, the level of gravity is still 9.04 m/s2. Only 8% less than the gravitational field on the Earth's surface.
Some references
• Minster O., Innocenti L., Mesland
D. Looking at science on board Eureca. ESA BR-80, 3-6, May 1993.
• Otto G.H., Schatz A. Methods to obtain and to simulate low-gravity conditions
Part I. Deutsche Forschungs- und Versuchsanstalt für Luft- und Raumfahrt
(DFVLR), Köln-Porz. Not dated.
• Pollard E.C. Theoretical studies on living systems in the absence of
mechanical stress. J. Theoret. Biol. 8, 113-123, 1965.
• Albrecht-Buehler G. Possible mechanisms of indirect sensing by cells.
ASGSB Bulletin 4(2), 25-34, July 1991.
• Moore D., Cogoli A. Gravitational and space biology at the cellular level.
In: Moore D, Bie P, Oser H, eds. Biological and medical research in space: an
overview of life sciences research in microgravity. Berlin : Springer-Verlag,
p. 1-106, 1996.